Selection sort in Java

by

Selection sort is one of the simple sorting algorithms. Its time complexity is O(n2).

Selection sort fundamental

  • Two nested loops
  • Involves swapping
  • At the end of each iteration, the lowest element is at the right position

Selection sort steps

As mentioned above, there are two loops in this algorithm. Essentially, the steps as below:

Selection sort step by step

Let’s consider an example to boost our understanding.

This is the initial array:

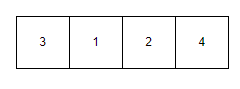
Initial array, selection sort

Iteration 1

We start the outer loop at index 0, assume it’s the index with the lowest value.

At this stage we have:

int i =0;
int lowest_index = 0;

Now compare all values from 0+1 to 4-1 (array length -1).

Compare 1 to 3, we found that 1 < 3 so we update the lowest index

lowest_index = 1;

Next we compare the next value to value at lowest_index. We found that 2 > 1 and 4 > 1 so there is no update to lowest_index needed.

At the end of this iteration, lowest_index = 1.

Since lowest_index != i, then we swap them.

This is the array at the first iteration:

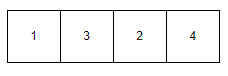
selection sort, first iteration

Iteration 2

At the beginning of this iteration, the values of i and lowest_index as below:

i =1;
lowest_index = 1;

The outer loop starts at index 1 (value 3).

The inner loop starts at index 2 (value 2).

Now we compare value at lowest_index with values at index 2. Since 2 < 3, we update the lowest index:

int lowest_index = 2;

We now compare the value at lowest_index with value at index 3 (4). Since 2 < 4, we don’t need to update the lowest index.

Since lowest_index != i, we swap them.

At the end of this iteration, we have:

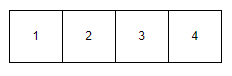
array at second iteration

It looks to us the array is sorted. However, the program doesn’t know that yet. We still need to do iteration 3.

Iteration 3

i =2;
lowest_index = 2;

Now we compare the value at index 3 (2 + 1 ) to the lowest index, since 3 < 4, we don’t need to update lowest_index.

There is no value left to compare, the algorithm stops here.

At the end of this iteration, the array looks like this:

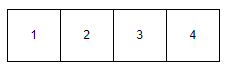
Final iteration

Selection sort implementation

Here is the implementation of selection sort algorithm in Java:

    private static int[] selection(int[] a) {
        //start the outer loop at 0
        for (int i = 0; i < a.length; i++) {
            //assign the lowest value to the current index
            int lowest = i;

            for (int k = i + 1; k < a.length; k++) {
                //if there is a value at k < value at lowest, update lowest to k
                if (a[k] < a[lowest]) {
                    lowest = k;
                }
            }
            //check if i != lowest, if so, swap them
            if (i != lowest) {
                swap(lowest, i, a);
            }
        }
        return a;
    }

Conclusion

As you can see, selection sort is an easy to implement sorting algorithm. Its time complexity is not ideal, though. In the worst case scenario, the time complexity of selection sort is O(n2) since it needs two nested loop to handle the logic.

Leave a Comment